Hidden Markov Model

Hidden Markov Model(HMM)是一种关于时序的概率模型，最初由 L. E. Baum 和其它一些学者发表在一系列的统计学论文中，随后在语言识别，自然语言处理以及生物信息等领域体现了很大的价值。本文通过个人的理解以及《统计学习方法》 中的公式推导对HMM的定义及其三个基本问题进行了简单的介绍。

Markov model

在介绍隐马尔可夫模型前我们先来介绍一下基础的马尔可夫链。马尔可夫链是一个随机模型描述序列可能的事件，其中每个事件的概率仅取决于在先前事件获得的状态 。粗略地说，以系统的当前状态为条件，其未来和过去的状态是相互独立的。
马尔可夫链的节点是状态，边是转移概率，是template CPD（条件概率分布）的一种有向状态转移表达。马尔可夫过程可以看做是一个自动机 ，以一定的概率在各个状态之间跳转。接下来以一阶马尔可夫链（first-order Markov chain）举例，N 次观测的序列的联合概率分布为：

$$p(x_1,...,x_n)=p(x_1)\prod_{i=2}^n p(x_n|x_{n-1}) \quad$$

由于每个事件发生的概率仅于前一件事件有关，即有：

$$p(x_n |x_1,…,x_{n-1} )=p(x_n |x_{n-1})$$

下面介绍马尔可夫链的一个重要性质，当n趋向于无穷时，p（Xn）趋向于一个定值。首先将每个事件的转移概率相整合成一个转移概率矩阵，假设每个事件的发生概率只与前一个事件的状态有关，共计n个状态的话，我们可以用一个n*n的矩阵P来表示转移概率，即 当我们有初始状态矩阵 时（ 表示初始状态为第i个状态的概率）则第n个状态的概率矩阵为 通过线性代数知识将转移概率矩阵做对角化，可得无穷个P矩阵相乘为一个常数，即马尔可夫链的极限收敛定理，马尔可夫链的这一性质对于其实际运用有重要的意义与作用。

HMM定义

在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在实际情况中，较为本质的状态转换通常是较为隐性即无法实际观测的，但是受该状态影响的变量是我们所可以观测的，由此，我们来介绍隐马尔可夫模型。在隐马尔可夫模型中，状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个隐性状态对于可观测的显性状态都有一概率分布，我们将这个概率称之为发射概率。
由此，如果我们有n个隐性状态的状态集合Q和有m个显性状态的观测集合V的话，假设I是长度为T的状态序列，O是对应的观测序列。我们就可设置转移一个$n \times n$的转移概率矩阵A和一个$m \times n$的发射概率矩阵B，π是初始状态概率向量：

$n \times n$的转移概率矩阵A:
$ \qquad a_{ij}=P(i_{t+1}=q_j│i_t=q_i ) \qquad i=1,…,N;j=1,…,N$

$m \times n$的发射概率矩阵B:
$ \qquad b_j (k)=P(o_t=v_k│i_t=q_j ) \qquad k=1,…,M;j=1,…,N$

π是初始状态概率向量:
$ \qquad π_i=P(i_1=q_i) \qquad i=1,…,N;j=1,…,N$

状态转移概率矩阵A与初始状态概率向量π确定了隐藏的马尔可夫链，生成不可观测的状态序列。发射概率矩阵B确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。隐马尔可夫模型就是由基本的A,B,π三个矩阵或向量加上具体的状态集合Q和观测序列V所构成的。
接下来我以维基百科上的一个经典例子来作为算法实际运用的实例 ：

“Consider two friends, Alice and Bob, who live far apart from each other and who talk together daily over the telephone about what they did that day. Bob is only interested in three activities: walking in the park, shopping, and cleaning his apartment. The choice of what to do is determined exclusively by the weather on a given day. Alice has no definite information about the weather, but she knows general trends. Based on what Bob tells her he did each day, Alice tries to guess what the weather must have been like.
Alice believes that the weather operates as a discrete Markov chain. There are two states, “Rainy” and “Sunny”, but she cannot observe them directly, that is, they are hidden from her. On each day, there is a certain chance that Bob will perform one of the following activities, depending on the weather: “walk”, “shop”, or “clean”. Since Bob tells Alice about his activities, those are the observations. The entire system is that of a hidden Markov model (HMM).
Alice knows the general weather trends in the area, and what Bob likes to do on average. In other words, the parameters of the HMM are known. 。”

这段稍显繁琐的文字可以转换成一张较为简洁易懂的状态转换图，如下：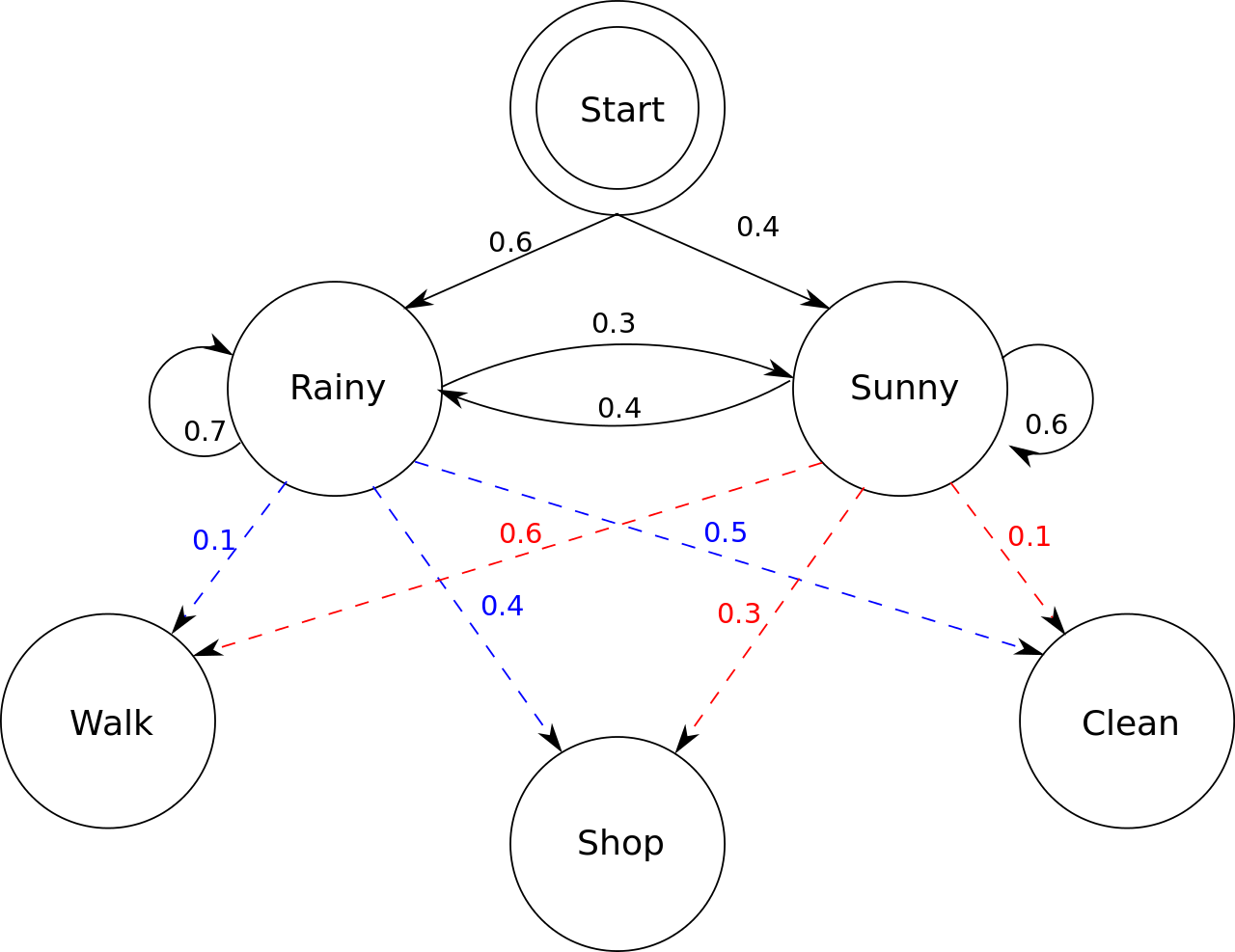

HMM基本问题

1. 概率计算问题：给定模型λ(A,B,π)和观测序列O,计算在模型λ下观测序列O出现的概率P(O|λ)为多少。
2. 学习问题：己知观测序列O,估计模型参数λ(A,B,π)使得在该模型下观测序列概率P(O|λ)最大。即用极大似然估计的方法估计参数。
3. 预测问题：也称为解码（decoding)问题。已知模型λ(A,B,π)和观测序列O，求对给定观测序列条件概率P(I|O)最大的状态序列I。即给定观测序列，求最有可能的对应的状态序列。

概率计算

1. 直接计算

   给定模型，求给定长度为T的观测序列的概率，直接计算法思路是枚举所有的长度T的状态序列，计算该状态序列与观测序列的联合概率（隐状态发射到观测），再用全概率公式对所有枚举项求和。在状态种类为N的情况下，一共有N^T种排列组合，每种组合计算联合概率的计算量为T，总的复杂度为O(T*N^T)，并不可取。

2. 前向计算

   前向算法的介绍
   前向计算中最为重要的一步的就是前向概率的设定，对于给定隐马尔可夫模型λ(A,B,π)，定义到时刻t为止的观测序列为O且状态为 的概率为前向概率，记作

   $$α_t (i)=P(o_1,o_2,…,o_t,i_t=q_i |λ)$$

   对于每一个时间点上的状态，都是用一个长度为n的概率矩阵来标记，转移到下一个状态前需要满足当前状态的观测值和已知观测序列一致，达成这个条件后即可正常转移到下一个状态，依次下去我们便可以递推地求得下一个前向概率及观测序列概率P(O|λ)

   • 初值 $$α_1 (i)=π_i b_i (o_1 ) \qquad i=1,…,N$$ 前向概率的定义中一共限定了两个条件，一是到当前为止的观测序列，另一个是当前的状态。所以初值的计算也有两项（观测和状态），一项是初始状态概率，另一项是发射到当前观测的概率。
   • 递推对t=1,2…T-1 $$\alpha_{t+1} (i)=[\sum_{j=1}^N \alpha_t (j) a_{ji}] b_i(o_{t+1}) \qquad i=1,…,N$$ 每次递推同样由两部分构成，括号中是当前状态为i且观测序列的前t个符合要求的概率，括号外的是状态i发射观测t+1的概率。
   • 终止 $$P(O|λ)=\sum_{i=1}^N[α_T (i)] \qquad i=1,…,N$$

   由于到了时间T，一共有N种状态发射了最后那个观测，所以最终的结果要用全概率公式将这些概率加起来。
   由于每次递推都是在前一次的基础上进行的，所以降低了复杂度。

   前向算法实例

   以之前天气的例子来说明前向算法，HMM模型可以写成：

   $$A=\begin{bmatrix} 0.7 & 0.3 \\\\ 0.4 & 0.6 \\\\ \end{bmatrix}$$ $$B=\begin{bmatrix} 0.1 & 0.4 & 0.5 \\\\ 0.6 & 0.3 & 0.1 \\\\ \end{bmatrix}$$ $$π=[0.6,0.4]^T$$ $$O=（散步，购物，扫除）$$

   假如我们想计算在（0.6,0.4）的初始状态下鲍比在未来三天分别按顺序做散步，购物，扫除的概率是多大，按照前向概率法计算，步骤如下：

   • 计算初值——初始状态下散步的前向概率：
     $\alpha_1 (1)=π_1 b_1 (o_1 )=0.06$
     $\alpha_1 (2)=π_2 b_2 (o_1 )=0.24$
   • 递推计算——本质还是转移概率乘上发射概率：
     $\alpha_2 (1)=\sum_{j=1}^2[\alpha_1 (j) a_{j1} ] b_1 (o_2 )=(0.042+0.096)×0.4=0.0552$
     $\alpha_2 (2)=\sum_{j=1}^2[\alpha_1 (j) a_{j2} ] b_2 (o_2 )=(0.018+0.144)×0.3=0.0198$
     $\alpha_3 (1)=\sum_{j=1}^2[\alpha_3 (j) a_{j1} ] b_1 (o_3 )=(0.03864+0.00792)×0.5=0.02328$
     $\alpha_3 (2)=\sum_{j=1}^2[\alpha_3 (j) a_{j2} ] b_2 (o_3 )=(0.01656+0.01188)×0.5=0.01422$
   • 终止：
     $P(O│λ)=\sum_{i=1}^N[\alpha_T (i)]=0.03750 $

3. 后向计算

   后向计算与前向计算相类似，只是定义了后向概率，再次不多做赘述。

Baum-Welch算法

假设给定训练数据只包含S个长度为T的观测序列O而没有对应的状态序列，目标是学习隐马尔可夫模型λ(A,B,π)的参数。我们将观测序列数据看作观测数据O，状态序列数据看作不可观测的隐数据I，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型：

$$P(O│λ)=\sum [P(O│I,λ)P(I|λ)]$$

它的参数学习可以由EM算法实现。这里简单介绍一下EM算法，EM算法即Expectation Maximization期望最大算法。这个算法的引入可以从极大似然估计入手，极大似然估计是对于单分布问题通过已经发生的事件来估计概率模型中的位置参数，但事实上存在很多多分布问题，你只有最后的观测序列结果，但对于其具体的隐藏状态一无所知，比如经典的高斯混合模型。这个时候我们所采取的措施是先假设一组隐藏状态概率，然后进行极大似然估计，再用极大似然估计后的参数将原参数更新，这样不断迭代直至最后估计值收敛，具体的公式推导与证明只给明出处 ，在此并不细说。

1. 确定完全数据的对数似然函数
   所有观测数据写成$O=(o_1,o_2,…,o_T)$,所有隐数据写成$I=(i_1,i_2,…,i_T)$，完全数据是$(O,I)=(o_1,o_2,…,o_T,i_1,i_2,…,i_T)$,。完全数据的对数似然函数是logP(O,I|λ)。

2. EM算法的E步：求Q函数

   $$Q(\lambda,\hat\lambda)=\sum_I[logP(O,I|\lambda)P(O,I|\hat\lambda)]$$

   其中，λ ̅是隐马尔可夫模型参数的当前估计值，λ是要极大化的隐马尔可夫模型参数。

   $$P(O,I│\lambda)=\pi_{i_1} b_{i_1} (o_1 ) a_{i_1 i_2 } b_{i_2} (o_2 )…a_{i_{T-1} i_T } b_{i_T} (o_T )$$

   这个式子从左到右依次是初始概率、发射概率、转移概率、发射概率……
   于是函数Q可以写成：

   $$Q(\lambda,\hat\lambda)=\sum_I[log\pi_(i_1 ) P(O,I|\lambda)]\\\\ +\sum_I(\sum_{t=1}^{T-1}[loga_{i_{t+1} \, i_t } ]) P(O,I│\hat\lambda)+\sum_I(\sum_{t=1}^Tlogb_{i_t}(o_t))P(O,I│\hat\lambda)$$

   式中求和都是对所有训练数据的序列总长度T进行的。这个式子是将$P(O,I│λ)=π_{i_1} b_{i_1} (o_1 ) a_{i_1 i_2} b_{i_2} (o_2 )…a_{i_(T-1) \, i_T } b_{i_T} (o_T )$代入$Q(\lambda ,\hat\lambda)=\sum_I logP(O,I\mid\lambda)P(O,I\mid\hat\lambda)$后，将初始概率、转移概率、发射概率这三部分乘积的对数拆分为对数之和，所以有三项。

3. EM算法的M步:极大化Q函数求模型参数λ(A,B,π)，由于要极大化的参数在Q函数表达式中单独地出现在3个项中，所以只需对各项分别极大化。
   第1项可以写成：

   $$\sum_Ilog\pi_{i_1} P(O,I|\hat\lambda)=\sum_{i=1}^Nlog\pi_i P(O,i_1=i|\hat\lambda)$$

   注意到$\pi_i$满足约束条件利用拉格朗日乘子法，写出拉格朗日函数。这个方法更简单明了的说法就是求条件极值，与微积分下册第五章第九节 所说内容几乎一致：

$$\sum_{i=1}^Nlog\pi_i P (O,i_1=i\mid\hat\lambda)+\gamma(\sum_{i=1}^N\pi_i-1)$$

对其求偏导数并令结果为0

$$\frac{\partial}{\partial\pi_i} [\sum_{i=1}^Nlog\pi_i P (O,i_1=i\mid\hat\lambda)+\gamma(\sum_{i=1}^N\pi_i-1)]=0$$

得到:

$$P(O,i_1=i│\hat\lambda)+\gamma\pi_i=0$$

这个求导是很简单的，求和项中非i的项对π_i求导都是0，logπ的导数是1/π，γ那边求导就剩下π_i自己对自己求导，也就是γ。等式两边同时乘以π_i就得到了上式。
对i求和得到γ：

$$\gamma=-P(O|\hat\lambda)$$

代入$P(O,i_1=i│\hat\lambda)+\gamma\pi_i=0$中得到：

$$\pi_i=\frac{P(o,i_1=i│\hat\lambda)}{P(O|\hat\lambda)}$$

同理可以求得：

$$a_{ij}=\frac{\sum_{i=1}^{T-1}P (O,i_t=i,i_{t+1}=j\mid\hat\lambda)}{\sum_{i=1}^{T-1}P (O,i_t=i\mid\hat\lambda)}$$ $$b_j (k)=\frac{\sum_{i=1}^TP (O,i_t=j\mid\hat\lambda )I(o_t=v_(k))}{\sum_{i=1}^{T-1}P (O,i_t=i\mid\hat\lambda ) }$$

预测算法

维特比算法

维特比算法实际是用动态规划解隐马尔可夫模型预测问题，即用动态规划求概率最大路径（最优路径）。这时一条路径对应着一个状态序列。
根据动态规划原理，最优路径具有这样的特性：如果最优路径在时刻t通过结点 ,那么这一路径从结点 到终点 的部分路径，对于从 到 的所有可能的部分路径来说，必须是最优的。因为假如不是这样，那么从 到 就有另一条更好的部分路径存在，如果把它和从 到达 的部分路径连接起来，就会形成一条比原来的路径更优的路径，这是矛盾的。依据这一原理，我们只需从时刻t=l开始，递推地计算在时刻t状态为i的各条部分路径的最大概率，直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率即为最优路径的概率P,最优路径的终结点 也同时得到。之后，为了找出最优路径的各个结点，从终结点 开始，由后向前逐步求得结点 ,得到最优路径——这就是维特比算法 。
换一种更加形象易懂的说法，假设将我们所有的状态拉成一个n*T的图，或者说一个每层有n个神经元，总共有T层的全连接神经网络。现在每一层的每个节点都会有来自上一层n个节点的连接，但我们只取其中概率最大的那一条边，将其他边全部“失活”，这样每个连接层都只剩n条边存在，不断递推直到最后一层为止，取最后一层概率最大的边为整个最优路径的概率，并不断回推得到最优路径。

维特比算法的实例

我们再以之前天气的例子来说明前向算法，将HMM模型写成：

$$A=\begin{bmatrix} 0.7 & 0.3 \\\\ 0.4 & 0.6 \\\\ \end{bmatrix}$$ $$B=\begin{bmatrix} 0.1 & 0.4 & 0.5 \\\\ 0.6 & 0.3 & 0.1 \\\\ \end{bmatrix}$$ $$π=[0.6,0.4]^T$$ $$O=（散步，购物，扫除）$$

假如在（0.6,0.4）的初始状态下，我们知道了Bob在接下来三天里分别按顺序做散步，购物，扫除，现在我们想知道那边的天气大概是什么样，按照维特比算法计算，步骤如下：

• 初始化：在t=1时，对每个状态i，求i观测o_1为散步的概率δ_1 (i)：
  $δ_1 (1)=0.6×0.1=0.06$
  $δ_1 (2)=0.4×0.6=0.24$
• 在t=2时，对每个状态i，i=1,2，求在t=1时状态为j观测为散步并在t=2时状态为i观测为购物的路径的最大概率，记录此最大概率为δ_2 (i)，则：
  $δ_2 (i)=max⁡[\delta_1 (j) a_{ji}]b_i (o_2) \qquad (1≤j≤2)$
• 通过该公式不断递推计算，我们可以很清楚的得到如下这张路径图：
  
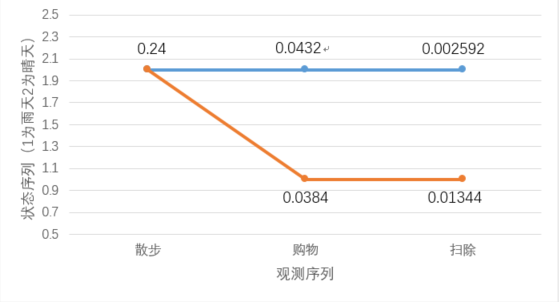
  所以最优路径为（晴天，雨天，雨天）发生概率为（即最大概率）为0.01344