图的储存结构:邻接矩阵,邻接表,十字链表,邻接多重表,边集数组
实现方式:矩阵,链表构成的数组*3,三元组
邻接矩阵(n个结点,构造n*n的矩阵,各点值可达为1,不可达为0)
当我们需要将权重赋在矩阵上时,各点值若可达,则为其权重;不可达则为∞(INT_MAX);对角元为0
邻接表(n个结点,构造有n个首结点的数组,每个首结点拉出一条含该首结点所有可达结点的链表)
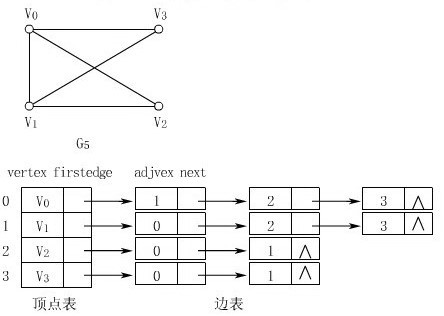
1 | |
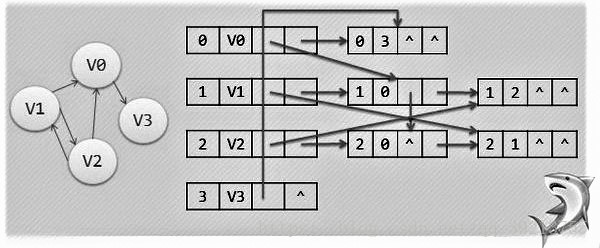
十字链表(有向图)
相比于邻接表,VNode多开了个指针域让你指向以该点为弧尾的第一个弧结点,便于同时求出度和入度,将原先的TNode变成有两个结点编号和两个指针域(一个指向弧头相同的下一条弧,一个指向弧尾相同的下一条弧)的Vex(弧结点)。
1 | |
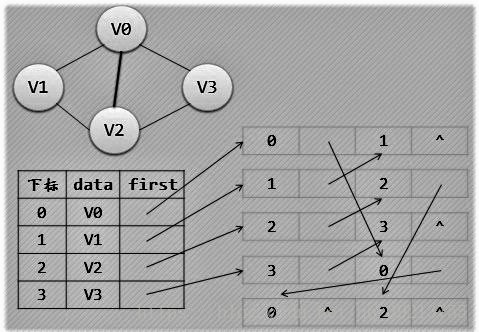
邻接多重表(无向图)
相比于邻接表,VNode不变,将原先的TNode变成有两个结点编号和两个指针域(一个指向下一条依附)的Vex(弧结点)
1 | |
(TIPS_对比:十字链表注重对边的操作,而邻接多重表更注重对点的操作)
边集数组(类似于三元组)
1 | |

