平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法)
AVL树:它左右的两个子树高度差的绝对值不超过1,且左右两个子树都是平衡二叉树。
引入
在说平衡二叉树之前,我们先需要谈谈二叉排序树,详见我之前在《排序》中所写。当排序树构建出来过于“畸形”,两边不对称,极端一点就是一路下来毫无分叉,那么显然,它的时间复杂度就是n,为了避免这种情况或者说,为了找寻最优情况,我们希望我们构建出来的二叉树可以两边对称平衡一下,使其树的深度为logn而非n,为此,我们引入平衡二叉树的概念。
调整(旋转)
当每次插入一个结点后,我们根据这棵树的现状对它进行旋转操作,可以简单的分为:
单旋
在A结点的左孩子的左子树或者右孩子的右子树上插入结点。
直接将B结点提上来,再把离A最近的子树滑给A。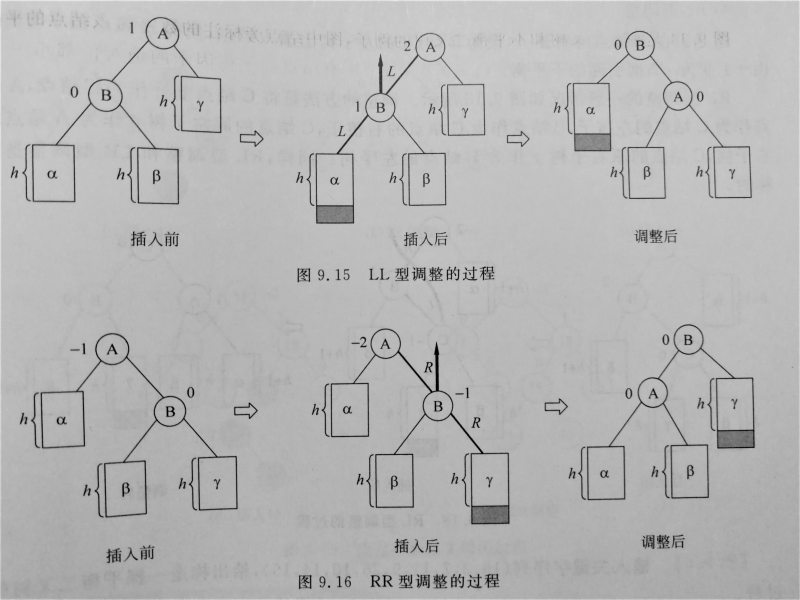
双旋
在A结点的左孩子的右子树或者右孩子的左子树上插入结点。
直接将C提到A、B之间,再把C的子树分别分给A、B所缺的位置。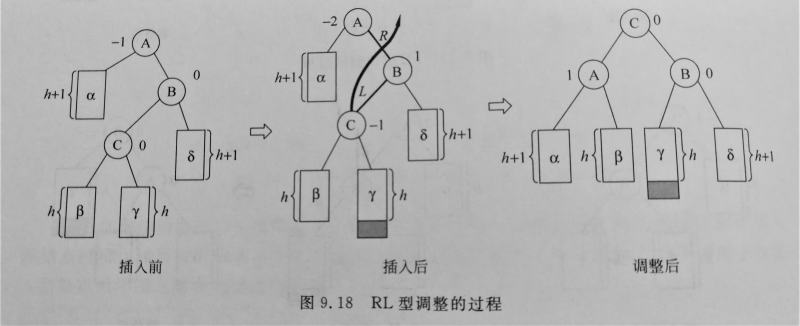
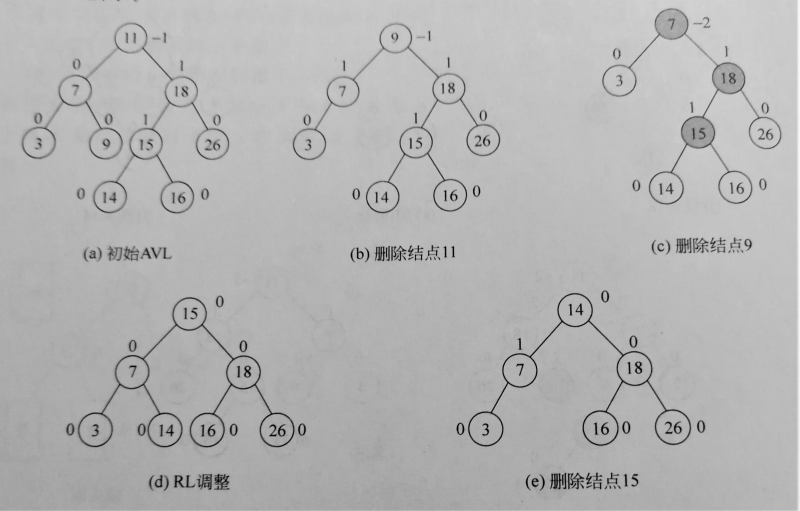
删除
查找
现在平衡树中查找到关键字相同的结点p
删除
分以下几种情况:
- 叶结点:直接删除就好
- 单分支结点:把后面那个孩子结点接上来就好啦
- 双分支结点:把这个双分支结点p的值,用其中序前驱结点q的值替代后,直接删掉结点q